Additional writings
In this lesson, we will continue to solve typical problems and transform various expressions containing radicals.
1. Repetition of theoretical facts
The key to solving all types of problems considered in this topic is the definition of the arithmetic root and its properties.
Let us recall the main definition once again.
Definition:
The n-th root of a non-negative number a is such a non-negative number b, which, when raised to the power of n, gives the number a.
Here is the mathematical notation of the definition:
For example: , because ; , because ,

2. Solution of examples for simplification and calculation
Let’s look at more complex examples.
Example 1 – simplify the expression:
Example 2 – calculate:
To perform the calculation, you need to convert the numerator, for this, in the second bracket, we represent composite numbers as prime numbers:
We get:
Let’s factorize the bracket by the grouping method:
After transformations, we get a fraction:
We have the right to reduce:
It is easy to notice in the resulting expression the formula for the difference of squares, let’s collapse it:
Example 3 – calculate:
Let’s calculate the inner root first:
After transformation, we got the expression:
Example 4 – simplify the expression:
It is important to notice the full square in the radical expression:
We get:
Comment: in order to highlight the full square, we have the right to represent a as , since the given expression contains , which means that a takes non-negative values.
Example 5 – simplify the expression:
Selecting a full square:
We get:
Comment: the number is negative, we have the right to open the module.
3. Equations with radicals, types, examples of solutions
It is important to be able to solve equations with radicals; consider the first type of such equations.
In order not to lose roots when solving and not to acquire new roots, some restrictions should be imposed. First of all, ODZ:. Further:
Note that when the second condition is met, the ODZ is observed automatically, so it can not be specified separately.
We got a mixed system, it contains an equation and an inequality. Note that it is not necessary to solve the inequality, it is enough to solve the equation and substitute the obtained roots into the inequality – check, because very often the inequality is very difficult or impossible to solve.
The second type of equations:
We indicate the domain of definition. ODZ:
To solve the given equation, you need to square it, we get:
To simplify finding the domain of definition, you can leave only one of the two inequalities, since two numbers are equal to each other and if one of them is greater than zero, then the second is also. We get systems for solving the equation:
or
Similarly to the first type, a mixed system is obtained, we can solve the equation and perform a check without completely solving the inequality.
Consider specific examples of equations.
Example 6:
This equation is equivalent to the system:
We solve the resulting system:
Answer:
This example can be solved in another way. Consider two functions – expressions on the right and left sides of the given equation:
The first function is monotonically decreasing (because there is a linear decreasing function under the root, its slope is less than zero), the second one is monotonically increasing.
Let’s illustrate what has been said:
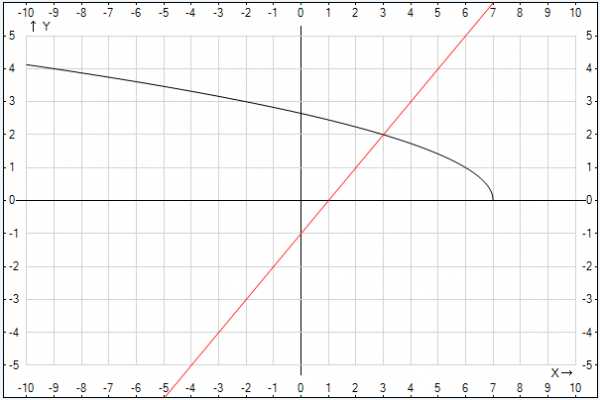
Rice. 1. Graphs of functions and
Since one of the functions is monotonically decreasing and the other is monotonically increasing, the equation has a unique solution, if a solution exists at all. Thus, if we find one root of a given equation, this will be a reasonable answer to the problem.
The root exists, from the figure we see that it is, to verify this, we substitute the found root into the original equation. We get the correct numerical equality.
Example 7:
We have an equivalent system:
We solve the resulting system:
Answer:
Example 8:
In this case, it is convenient to perform a change of variables.
Denote , square, we get:
We get the equation:
We do not lose the constraint:
We solve the resulting quadratic equation in any way, we find the roots:
or
We discard the extra root, it remains
In this way,
So, we have considered the solution of problems and equations containing radicals.
